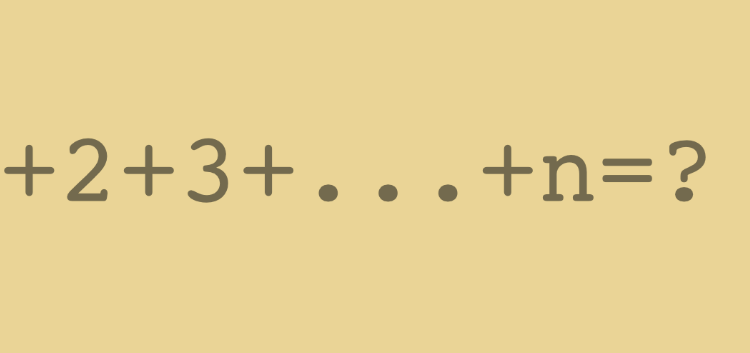At the very beginning, let us learn what is a Sequence. A sequence is a set of numbers written in a particular order. For example, the numbers 2, 4, 6, 8, 10, …. Seem to be occurring by following a rule. This is a sequence of the even numbers. The sequence starts with the even number 2, and then the next number is obtained by adding 2 to the previous number in the series.

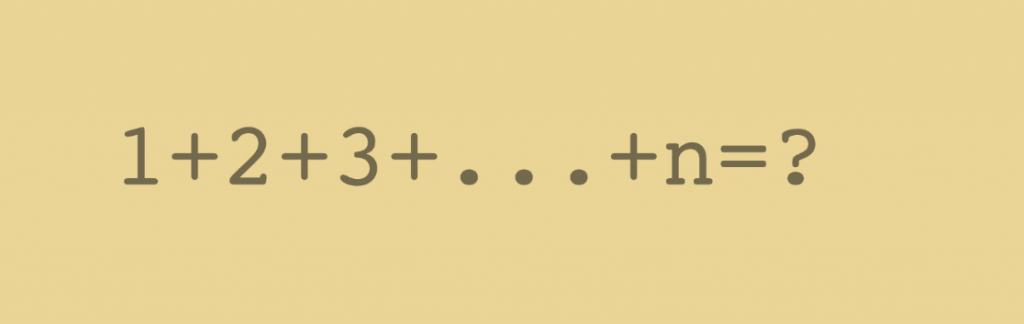
This is the first concept you are taught in CBSE class 10 maths arithmetic progressions.

Let us take another example: 1, 8, 27, 64, 125, ….

This is the sequence where the numbers are cubed. 2, -2, 2, -2, 2, -2, 2, -2,….. also happens to be a sequence that has an alternating pattern of 2 and -2.

In all of these sequences, the dots at the end indicate that the sequence runs to infinity.

However, you may also have a finite sequence, where the number of terms is given. For example, 2, 4, 6, 8 is a finite sequence of 4 terms, 1, 8, 27, 64, 125 is a finite sequence of 5 terms.

Similarly, 1,2,3,4,5,6,……n is also a finite sequence where the last term is n. the dots here indicate that the numbers in between have not been explicitly written.

Let us tell you about a very special infinite sequence, called the Fibonacci Sequence. It goes like this:

1, 1, 2, 3, 5, 8, ….

Each term, as you can observe, is the sum of the two previous numbers.

To generalize the concept, let us use algebraic expressions to denote the terms of the sequence. So, if in a sequence, the first term in t₁ , the second term is t₂ and so on, and t_n is the nth term, then the sequence may be written as:

t_1, t_2, t₃, ….., t_n

Here also the sequence is finite, comprising n number of terms. Now, let us represent the Fibonacci sequence using the algebraic expressions:

t_n= t_{n – 1} + t_{n – 2}, which implies that each term is the sum of the two terms just before it.

Understanding the concept of a series

A series is a number that we obtain when we add up all the terms in a sequence. For example, for the sequence t_1, t_2, t₃, ….., t_n, the series will be:

t_{1 +} t_{2 +}  t_{3 +}  …..+t_n

now, if we denote the sum thus obtained by S_n.

In the sequence, , 1,2,3,4,5,6,…n,

S₁ = 1, as it denotes the sum of the first term

S₂ = 1 + 2 = 3. Similarly, S₃ = 1 + 2 + 3 = 6 and so on.

Understanding the Concept of Arithmetic Progressions

Let us start to understand the concept with the help of an example:

0, 10, 20, 30, 40. In this case, you just look at the sequence and get to understand how it has been formed. There is a number added to the first term, and thus the second term is obtained. So are the 3^rd and the 4^th terms. Thus, the difference between the terms in a sequence is a constant.

Any sequence that has a constant difference (which can be either positive or negative) between consecutive terms, is called an arithmetic progression or an AP.

Now you work out the sums in the NCERT textbook and find out the NCERT solutions for Class 10^th maths chapter 5 on Arithmetic Progressions.